SGDR: Stochastic Gradient Descent with Warm Restarts
Ilya Loshchilov, Frank Hutter, 2016
Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates
Leslie N. Smith, Nicholay Topin, 2017
Research Topic
- Category (General): Deep Learning
- Category (Specific): Hyper Tuning, Optimization
Paper summary
SGDR
- Partial warm restarts improve rate of convergence, often used in gradient-free optimization.
- Propose a warm restart technique for stochastic gradient descent.
- Study its performance on CIFAR-10/100
- Show that this technique improve its anytime performance when training deep neural network:
- SGD with warm restarts requires 2× to 4× fewer epochs than the currently-used learning rate schedule schemes to achieve comparable or even better results
Super-convergence
- Introduce “Super-convergence” term: where neural networks can be train and converge much faster than standard training methods.
- Propoce a way to achieve super-convergence: one-cycle policy + large learning rate.
- Use Hessian Free optimization method to produce an estimate of the optimal learning rate.
- Study its performance on CIFAR-10/100, MNIST, Imagenet with various model.
- Show that this phenomenon can also happen when the amount of labeled training data is limited but still boost the model performance.
- Mostly all of these are mentioned in the previous recap, so it will not be discussed more in the sections below.
Explain Like I’m 5 (ELI5) 👶👶👶
SGDR
- Just like a normal person works everyday. You start the day with maximum effort, but then time goes by you feel tired and the productivity reduces. You go home, rest. The next day, you’re recharged and start the cycle once again.
Super-convergence
- As a result of CLR, super-convergence is born.
Issues addressed by the paper
SGDR
- Despite of the existance of advanced optimization methods like Adam, AdaDelta, SOTA result on CIFAR-10/100, ImageNet still based on SGD with momentum, associated with Resnet model.
- Current way to get out of the plateau while using SGD is LR scheduler and L2 regularization.
- They want to break through and produce a new approach to SGD.
Super-convergence
- They found a way to train DNN faster and achieve better performance.
- Large LR regularizes training, so other regularization method should be reduced to maintain optimal balance of optimization
- Hessian-free optimization method estimates optimal LR, demonstrating that large LR find wide, flat minima.
Approach/Method
SGDR
- SGDR simulates a new warm-started run/restart of SGD after \(T_{i}\) epochs are performed.
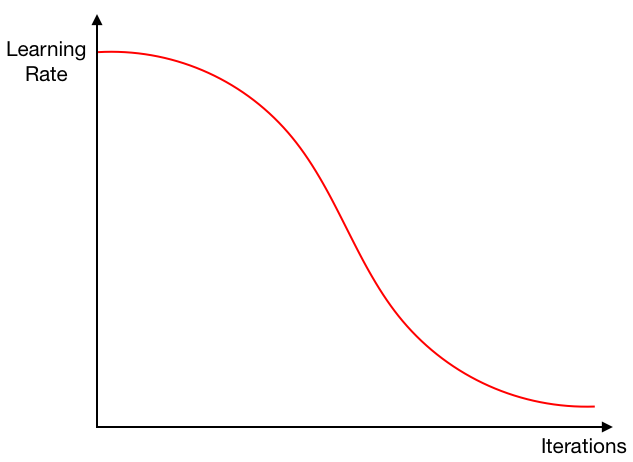
- Learning rate is calculated by cos annealing function.
- \(\eta\): learning rate.
- \(T_{cur}\): how many epochs passed since the restart.
-
\(T_{i}\): how mane epochs for a restart, you can leave it constant or increase over-time.
- How the learning rate looks after training:
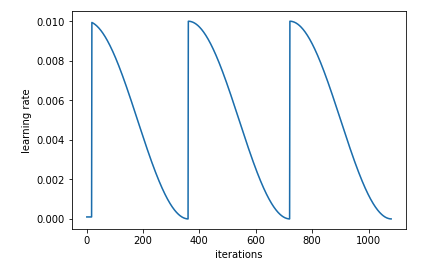
Best practice
SGDR
- Start with small \(T_{i}\), then increase it by factor of \(T_{mult}\) at every start.
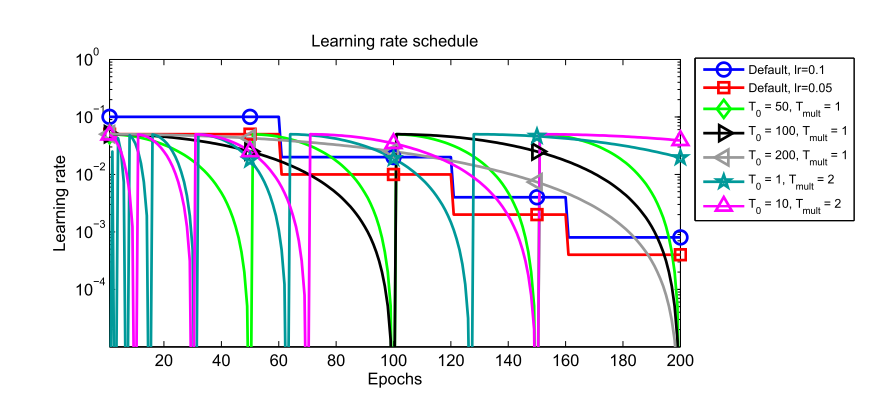
- Decreate max_lr and min_lr at every new start may increase performance.
- Stop training when current learning rate is equal to min_lr.
- SGDR allows to train larger network.
Results
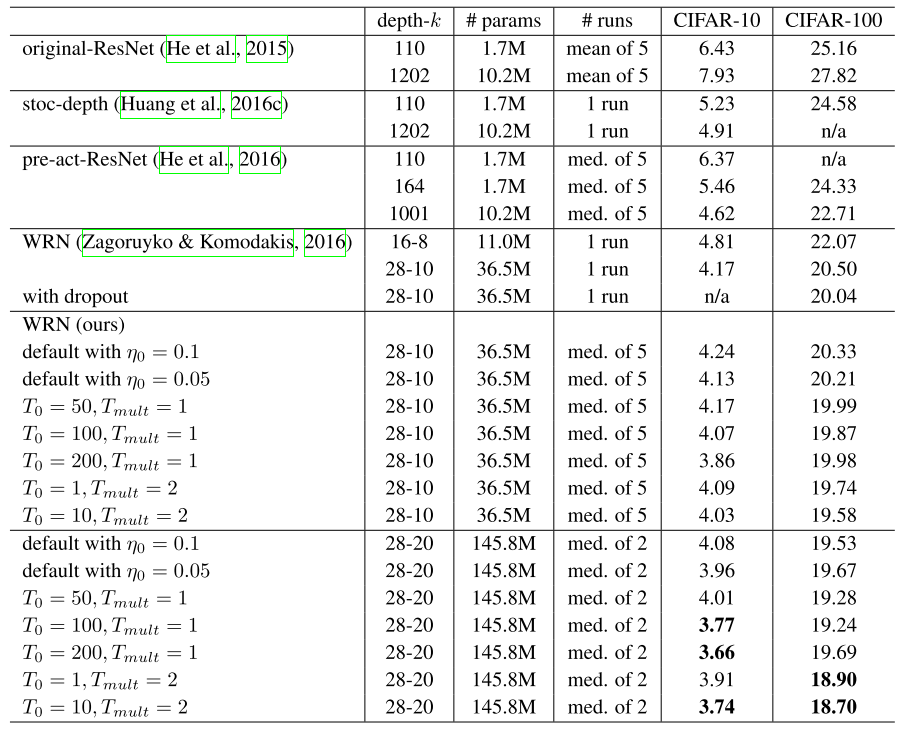
- SGDR technique helps the author to surpass the SOTA at the time with much faster computational time.
Conclusions
The author’s conclusions
- Our SGDR simulates warm restarts by scheduling the learning rate to achieve competitive results on CIFAR-10 and CIFAR-100 roughly two to four times faster, achieved new state- of-the-art results with SGDR.
- SGDR might also reduce the problem of learning rate selection because the annealing and restarts of SGDR scan / consider a range of learning rate values.
Rating

My Conclusion
- Another technique can be considered when training in new project, should quick test overall before stick to one and go deeper.
Paper implementation
Cos Annealing
def sched_cos(start, end, T_cur, T_i):
return start + (1 + math.cos(math.pi*(T_cur / T_i))) * (end-start) / 2SGDR
def step(self, epoch=None):
if epoch is None and self.last_epoch < 0:
epoch = 0
if epoch is None:
epoch = self.last_epoch + 1
self.T_cur = self.T_cur + 1
if self.T_cur >= self.T_i:
self.T_cur = self.T_cur - self.T_i
self.T_i = self.T_i * self.T_mult
else:
if epoch < 0:
return
if epoch >= self.T_0:
if self.T_mult == 1:
self.T_cur = epoch % self.T_0
else:
n = int(math.log((epoch / self.T_0 * (self.T_mult - 1) + 1), self.T_mult))
self.T_cur = epoch - self.T_0 * (self.T_mult ** n - 1) / (self.T_mult - 1)
self.T_i = self.T_0 * self.T_mult ** (n)
else:
self.T_i = self.T_0
self.T_cur = epoch
self.last_epoch = math.floor(epoch)
self.lr = sched_cos(self.base_lr, self.max_lr, self.T_cur, self.T_i)Cited references and used images from:
- https://towardsdatascience.com/https-medium-com-reina-wang-tw-stochastic-gradient-descent-with-restarts-5f511975163
- https://arxiv.org/abs/1608.03983
- Pytorch library