MixUp: Beyond empirical risk minimization
Zhang, Hongyi Cisse, Moustapha Dauphin, Yann N.Lopez-Paz, David, 2018
Research Topic
- Category (General): Deep Learning
- Category (Specific): Data Augmentation
Paper summary
- Introduce a new data augmentation method: MixUp, which helps:
- Improve generalization of neural network architectures.
- Reduces memorization of corrupt labels.
- Increases the robustness to adversarial learning.
- Stabilize the training of GANs.
Explain Like I’m 5 (ELI5) 👶👶👶
- Well this gif sums up pretty well…

Issues addressed by the paper
- As the model is being trained by minimizing the loss/objective function using a known set of training data (Empirical Risk Minimization), it can choose to memorize the training data rather than generalize it, even when in the presence of strong regularization. So the model will perform terribly when evaluating on examples outside the training distribution.
- Normal data augmentation can help model to improve generalization, but it requires costly computations, and also needs human experts to decide how to augment the data.
Approach/Method
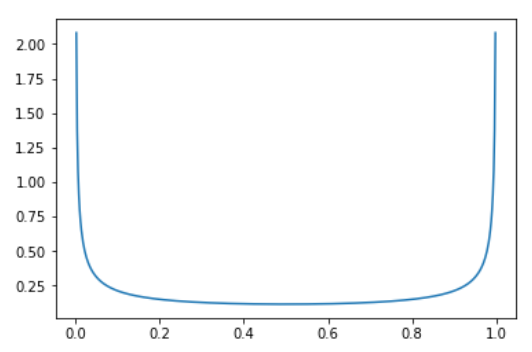
- Core idea: Linear interpolate (lerp) two images and its labels together, then do it for the whole batch. Use soft label for better performance. How much to interpolate is used by a number call
lambdagenerated by Beta Distribution.new_image = lambda * image_1 + (1-lambda) * image_2 new_label = lambda * label_1 + (1-lambda) * label_2 lambdais sampled from symmetric Beta distribution (having same \(\alpha\) and \(\beta\) value), which looks like the following image. This distribution makes sure that the new image will most of the time be close only to the first or the second picture. Only sometimes both images have the same intensity (of course if in a case of multicategorical, other label will be 0).
- They tried multiple ways to pick images:
- Use 2 different dataloader, take one of each then interpolate -> good mix, but need 2 loaders which takes more time to run.
- Use more than two pictures to mix: non-significant improvement, but increases the computation cost.
- Use only 1 dataloader, then mixup the batch and its shuffled-version -> may have duplicates, but peforms equally well -> RECOMMEND.
Result
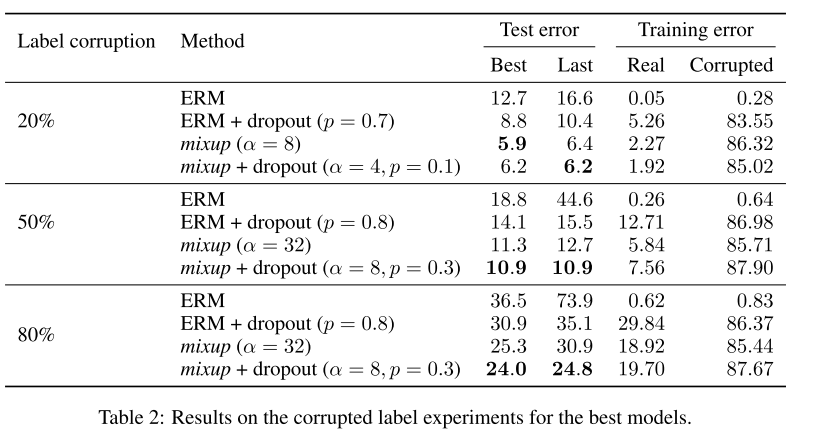
- Reduces the amount of undesirable oscillations when predicting outside the training examples, also makes memorization more difficult to achieve (generalizes better). The author had make tests by training both normal (ERM) and mixup model against randomly corruptled labels:
- As you can see, the ERM model starts to overfit the corrupted labels when the LR starts to slow down to fine tune.
- mixup model doesn’t do the same, so when it’s tested against the real label, it still performs fairly well -> not overfitted.
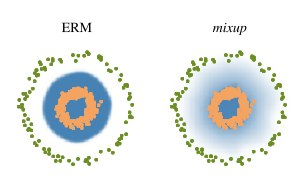
- Leads to decision boundaries that transition linearly from class to class, providing a smoother estimate of uncertainty:
- In the ERM model, if an adversarial example (class orange) can push through the blue boundary, the model will definately determine that example is class 0.
- On the other hand, since mixup model produce a smooth boundary, it may still classify that example correctly.
- Significantly improve the robustness of neural networks without hindering the speed of ERM.
Best practice
- \(\alpha \in [0.1, 0.4]\) usually performs well, whereas larger \(\alpha\) may lead to underfitting.
- When using mixup, use larger neural network and also train longer for better result.
- mixup + dropout performs very nicely together (produced SOTA in the paper).
Hidden gems💎💎💎
- For normal data augmentation, one usually uses rotation, translation, cropping, resizing, flipping and random erasing to enforce visually plausible invariances in the model through the training data.
Conclusions
Rating

Paper implementation
- Using Pytorch Lightning Callback system, inspired by fastai implementation.
class MixLoss(nn.Module): def __init__(self, old_lf, mixup_cb): super().__init__() self.old_lf = old_lf self.mixup_cb = mixup_cb def forward(self, pred, yb): if self.mixup_cb.pl_module.testing: return self.old_lf(pred, yb) with NoneReduce(self.old_lf) as lf: self.mixup_cb.yb_1 = self.mixup_cb.yb_1.to(pred.device) self.mixup_cb.lam = self.mixup_cb.lam.to(pred.device) loss = torch.lerp(lf(pred, self.mixup_cb.yb_1), lf(pred,yb), self.mixup_cb.lam) return reduce_loss(loss, getattr(self.old_lf, 'reduction', 'mean')) class MixupDict(Callback): def __init__(self, alpha=0.4): super().__init__() self.distrib = Beta(tensor(alpha), tensor(alpha)) def on_train_start(self, trainer, pl_module): self.old_lf = pl_module.loss_func self.loss_fnc = MixLoss(self.old_lf, self) pl_module.loss_func = self.loss_fnc self.pl_module = pl_module def _mixup(self, batch, logger, log_image=False, pre_fix='train'): xb, yb = batch["img"], batch["label"] bs = yb.size(0) # Produce "bs" probability for each sample lam = self.distrib.sample((bs,)).squeeze() # Get those probability that >0.5, so that the first img (in the nonshuffle batch) has bigger coeff # Which avoid duplication mixup lam = torch.stack([lam, 1-lam], 1) self.lam = lam.max(1)[0] # Permute the batch shuffle = torch.randperm(bs) xb_1, self.yb_1 = xb[shuffle], yb[shuffle] nx_dims = len(xb.size()) weight = unsqueeze(self.lam, n=nx_dims-1) x_new = torch.lerp(xb_1, xb, weight=weight) if log_image: grid = torchvision.utils.make_grid(x_new) logger.experiment.add_image(pre_fix + 'mixup', grid) grid_g = torchvision.utils.make_grid(xb) logger.experiment.add_image(pre_fix + 'norm', grid_g) dif = abs(xb - x_new) grid_d = torchvision.utils.make_grid(dif) logger.experiment.add_image(pre_fix + 'dif', grid_d) return x_new def on_train_batch_start(self, trainer, pl_module, batch, batch_idx, dataloader_idx): x = self._mixup(batch, trainer.logger) batch["img"] = x def on_validation_start(self, trainer, pl_module): pl_module.loss_func = self.old_lf def on_validation_end(self, trainer, pl_module): pl_module.loss_func = self.loss_fnc def on_fit_end(self, trainer, pl_module): pl_module.loss_func = self.old_lf